B+树索引

数据页可以组成一个双向链表，而每个数据页中的记录会按照主键值从小到大的顺序组成一个单向链表，每个数据页都会为存储在它里边儿的记录生成一个页目录，在通过主键查找某条记录的时候可以在页目录中使用二分法快速定位到对应的槽，然后再遍历该槽对应分组中的记录即可快速找到指定的记录。页和记录的关系示意图如下：

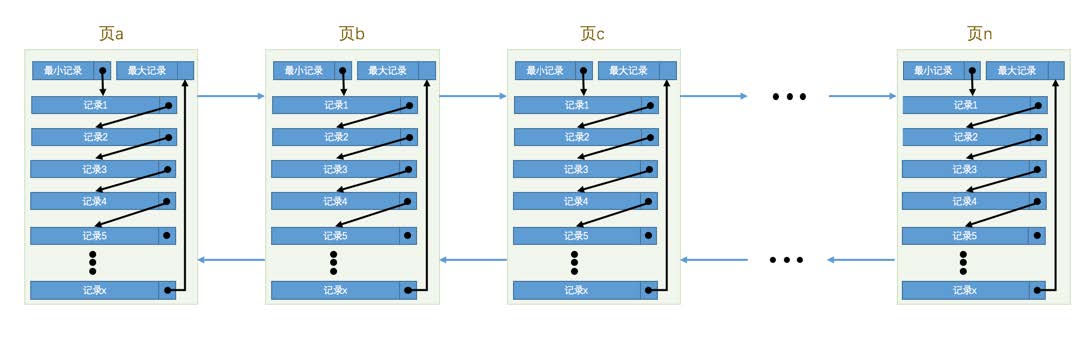
其中页a、页b、页c ... 页n 这些页可以不在物理结构上相连，只通过双向链表相关联。

为了故事的顺利发展，我们先建一个表：

CREATE TABLE index_demo(
    c1 INT,
    c2 INT,
    c3 CHAR(1),
    PRIMARY KEY(c1)
) ROW_FORMAT = Compact;

1. InnoDB中的索引方案

MySQL复用了之前存储用户记录的数据页来存储目录项。

为了和用户记录做一下区分，我们把这些用来表示目录项的记录称为目录项记录。InnoDB通过记录头信息里的record_type属性来区分一条记录是普通的用户记录还是目录项记录：

• 0：普通的用户记录
• 1：目录项记录
• 2：最小记录
• 3：最大记录

把目录项放到数据页中的样子就是这样：

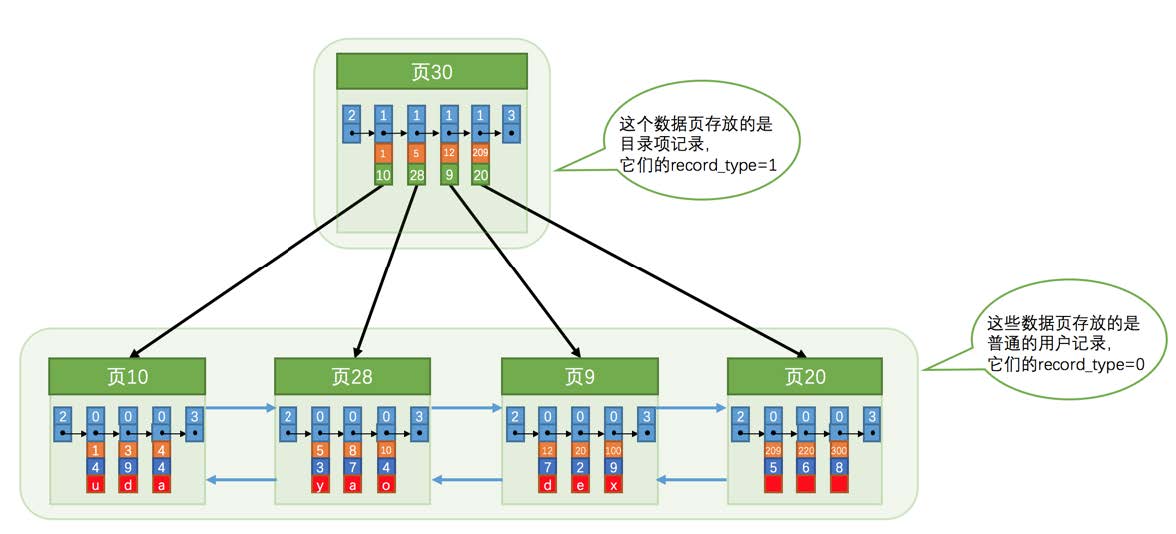
从图中可以看出来，我们新分配了一个编号为30的页来专门存储目录项记录。这里强调一遍目录项记录的特点：

• 目录项记录的record_type值是1。

• 目录项记录只有主键值和页的编号两个列。

• 只有在存储目录项记录的页中的主键值最小的目录项记录的min_rec_mask值为1，其他别的记录的min_rec_mask值都是0。

如果以查找主键为20的记录为例，根据某个主键值去查找记录的步骤就可以大致拆分成下边两步：

1. 先到存储目录项记录的页，也就是页30中通过二分法快速定位到对应目录项，因为12 < 20 < 209，所以定位到对应的记录所在的页就是页9。

2. 再到存储用户记录的页9中根据二分法快速定位到主键值为20的用户记录。

但是一个页只有16KB大小，以至于一个数据页不足以存放所有的目录项记录的话，MySQL会新增一个存储目录项记录的页。

我们假设一个存储目录项记录的页最多只能存放4条目录项记录，所以如果此时我们再向上图中插入一条主键值为320的用户记录的话，那就需要分配一个新的存储目录项记录的页：

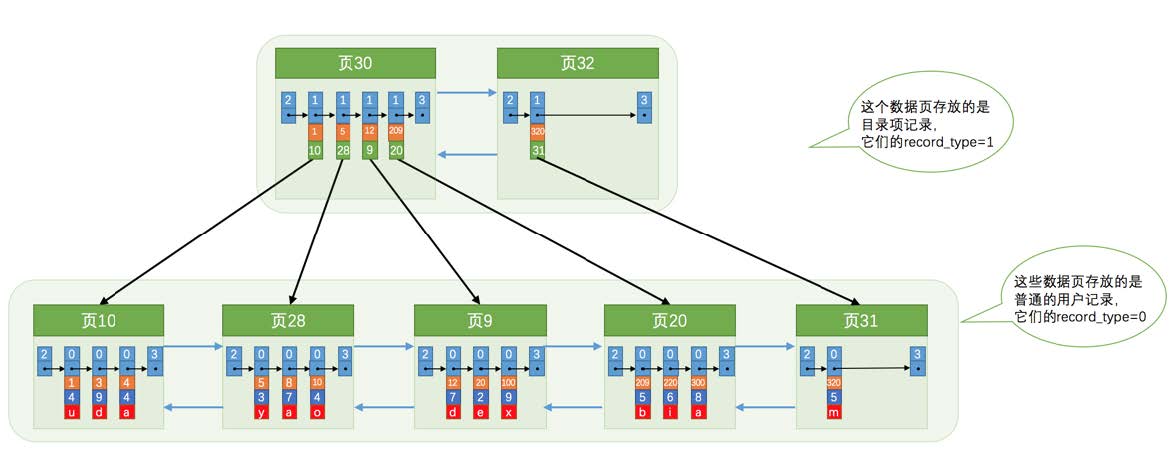
从图中可以看出，我们插入了一条主键值为320的用户记录之后需要两个新的数据页：

• 为存储该用户记录而新生成了页31。

• 假设原先存储目录项记录的页30的容量已满，所以不得不需要一个新的页32来存放页31对应的目录项。

如果我们想根据主键值查找一条用户记录大致需要3个步骤，以查找主键值为20的记录为例：

1. 确定目录项记录页。

2. 通过目录项记录页确定用户记录真实所在的页。

3. 在真实存储用户记录的页中定位到具体的记录。

为了定位存储目录项记录的页，我们为这些存储目录项记录的页再生成一个更高级的目录，就像是一个多级目录一样，大目录里嵌套小目录，小目录里才是实际的数据，所以现在各个页的示意图就是这样子：

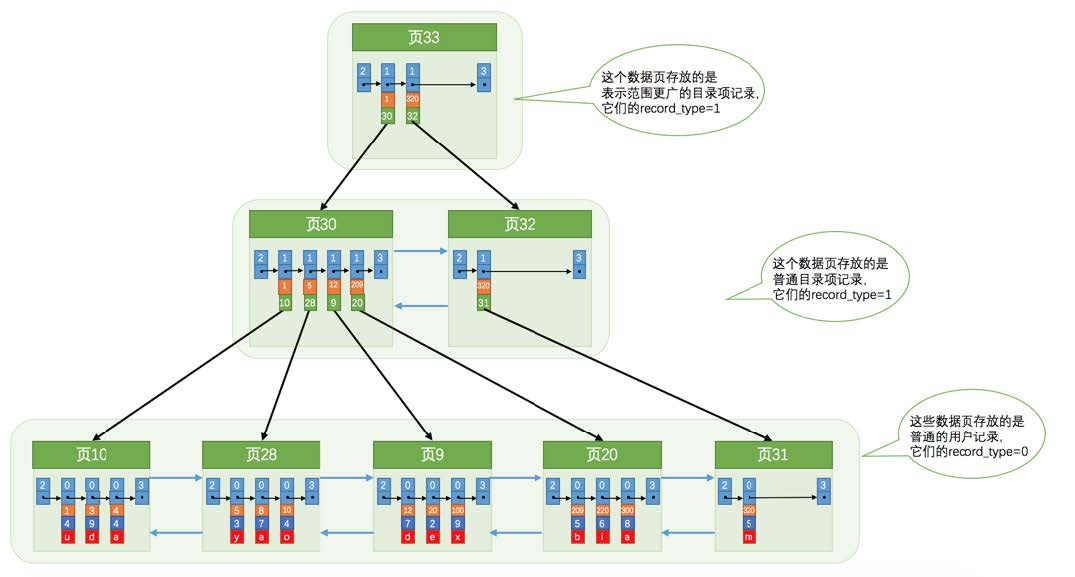
随着表中记录的增加，这个目录的层级会继续增加，如果简化一下，那么我们可以用下边这个图来描述它：

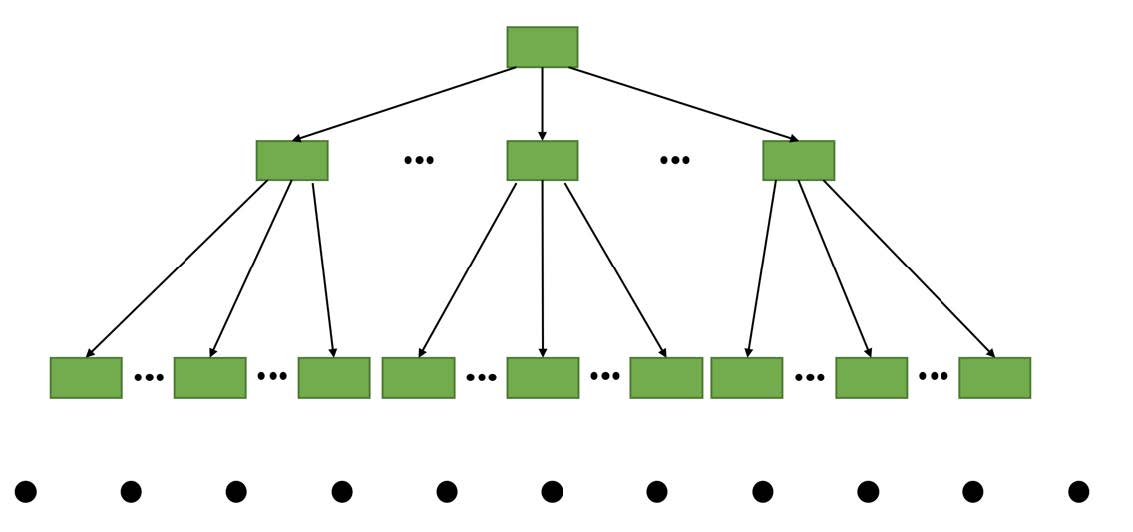
这玩意儿像不像一个倒过来的树呀，上头是树根，下头是树叶！其实这是一种组织数据的形式，或者说是一种数据结构，它的名称是B+树。

B+树的最底层的节点称为叶子节点或叶节点，其余用来存放目录项的节点称为非叶子节点或者内节点，其中B+树最上边的那个节点也称为根节点。

MySQL规定最下边的那层，也就是存放我们用户记录的那层为第0层，之后依次往上加。一般情况下，我们用到的B+树都不会超过4层，那我们通过主键值去查找某条记录最多只需要做4个页面内的查找（查找3个目录项页和一个用户记录页），又因为在每个页面内有所谓的Page Directory（页目录），所以在页面内也可以通过二分法实现快速定位记录。

1.1. 聚簇索引

聚簇索引：只能在搜索条件是主键时生效。

我们上边介绍的B+树本身就是一个目录，或者说本身就是一个索引。它有两个特点：

1. 使用记录主键值的大小进行记录和页的排序，这包括三个方面的含义：

   • 页内的记录是按照主键的大小顺序排成一个单向链表。

   • 各个存放用户记录的页也是根据页中用户记录的主键大小顺序排成一个双向链表。

   • 存放目录项记录的页分为不同的层次，在同一层次中的页也是根据页中目录项记录的主键大小顺序排成一个双向链表。

2. B+树的叶子节点存储的是完整的用户记录。

   • 完整的用户记录：就是指这个记录中存储了所有列的值（包括隐藏列）。

具有这两种特性的B+树称为聚簇索引，所有完整的用户记录都存放在这个聚簇索引的叶子节点处。这种聚簇索引并不需要我们显式的使用INDEX语句去创建，InnoDB存储引擎会自动的为我们创建聚簇索引。在InnoDB存储引擎中，聚簇索引就是数据的存储方式（所有的用户记录都存储在了叶子节点），也就是所谓的索引即数据，数据即索引。

1.2. 二级索引

对于其他的列作为搜索条件时，通过多建几棵B+树，不同的B+树中的数据采用不同的排序规则来进行索引查找。

假如说我们用c2列的大小作为数据页、页中记录的排序规则，再建一棵B+树，效果如下图所示：

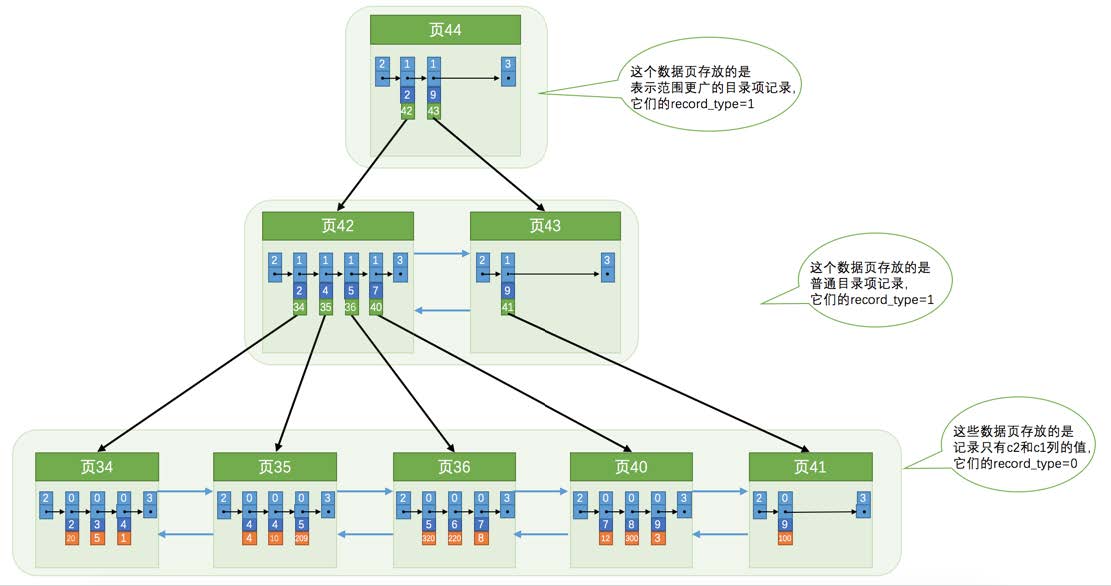
• 这个**B+**树与上边介绍的聚簇索引有几处不同：

  • 使用记录c2列的大小进行记录和页的排序，这包括三个方面的含义：

    • 页内的记录是按照c2列的大小顺序排成一个单向链表。

    • 各个存放用户记录的页也是根据页中记录的c2列大小顺序排成一个双向链表。

    • 存放目录项记录的页分为不同的层次，在同一层次中的页也是根据页中目录项记录的c2列大小顺序排成一个双向链表。

  • B+树的叶子节点存储的并不是完整的用户记录，而只是c2列+主键这两个列的值。

  • 目录项记录中不再是主键+页号的搭配，而变成了c2列+页号的搭配。

以查找c2列的值为4的记录为例，查找过程如下：

1. 确定目录项记录页，根据根页面，也就是页44，可以快速定位到目录项记录所在的页为页42。

2. 通过目录项记录页确定用户记录真实所在的页。在页42中可以快速定位到实际存储用户记录的页，但是由于c2列并没有唯一性约束，所以c2列值为4的记录可能分布在多个数据页中，又因为2 < 4 ≤ 4，所以确定实际存储用户记录的页在页34和页35中。

3. 在真实存储用户记录的页中定位到具体的记录。到页34和页35中定位到具体的记录。

4. 但是这个B+树的叶子节点中的记录只存储了c2和c1（也就是主键）两个列，所以我们必须再根据主键值去聚簇索引中再查找一遍完整的用户记录。

如果我们想根据c2列的值查找到完整的用户记录的话，仍然需要到聚簇索引中再查一遍，这个过程也被称为回表。

为什么我们还需要一次回表操作呢？直接把完整的用户记录放到叶子节点不就好了么？你说的对，如果把完整的用户记录放到叶子节点是可以不用回表，但是太占地方了呀～相当于每建立一棵B+树都需要把所有的用户记录再都拷贝一遍，这就有点太浪费存储空间了。因为这种按照非主键列建立的B+树需要一次回表操作才可以定位到完整的用户记录，所以这种B+树也被称为二级索引（英文名secondary index），或者辅助索引。由于我们使用的是c2列的大小作为B+树的排序规则，所以我们也称这个B+树为为c2列建立的索引。

1.3. 联合索引

我们也可以同时以多个列的大小作为排序规则，也就是同时为多个列建立索引，比方说我们想让B+树按照c2和c3列的大小进行排序，这个包含两层含义：

• 先把各个记录和页按照c2列进行排序。
• 在记录的c2列相同的情况下，采用c3列进行排序

为c2和c3列建立的索引的示意图如下：

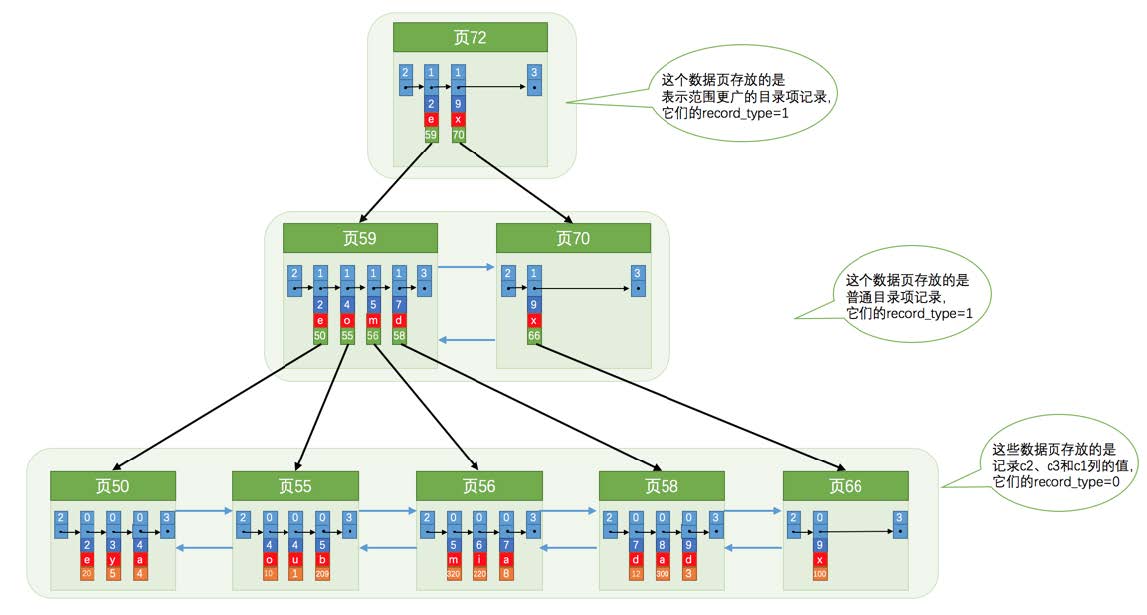
如图所示，我们需要注意一下几点：

• 每条目录项记录都由c2、c3、页号这三个部分组成，各条记录先按照c2列的值进行排序，如果记录的c2列相同，则按照c3列的值进行排序。
• B+树叶子节点处的用户记录由c2、c3和主键c1列组成。

以c2和c3列的大小为排序规则建立的B+树称为联合索引。

2. InnoDB的B+树索引的注意事项

2.1. 根页面万年不动窝

我们前边介绍B+树索引的时候，为了大家理解上的方便，先把存储用户记录的叶子节点都画出来，然后接着画存储目录项记录的内节点，实际上B+树的形成过程是这样的：

• 每当为某个表创建一个B+树索引的时候，都会为这个索引创建一个根节点页面。最开始表中没有数据的时候，每个B+树索引对应的根节点中既没有用户记录，也没有目录项目录。

• 随后向表中插入用户记录时，先把用户记录存储到这个根节点中。

• 当根节点中的可用空间用完时继续插入记录，此时会将根节点中的所有记录复制到一个新分配的页，比如页a中，然后对这个新页进行页分裂的操作，得到另一个新页，比如页b。这时新插入的记录根据键值（也就是聚簇索引中的主键值，二级索引中对应的索引列的值）的大小就会被分配到页a或者页b中，而根节点便升级为存储目录项记录的页（由原先的存储用户记录的数据页转换为存储目录项记录的页）。

这个过程需要大家特别注意的是：**一个B+树索引的根节点自诞生之日起，便不会再移动。**这样只要我们对某个表建立一个索引，那么它的根节点的页号便会被记录到某个地方，然后凡是InnoDB存储引擎需要用到这个索引的时候，都会从那个固定的地方取出根节点的页号，从而来访问这个索引。

2.2. 内节点中目录项记录的唯一性

我们知道B+树索引的内节点中目录项记录的内容是索引列 + 页号的搭配，但是这个搭配对于二级索引来说有点儿不严谨。还拿index_demo表为例，假设这个表中的数据是这样的：

c1	c2	c3
1	1	'u'
3	1	'd'
5	1	'y'
7	1	'a'

为了让新插入记录能找到自己在那个页里，我们需要保证在B+树的同一层内节点的目录项记录除页号这个字段以外是唯一的。所以对于二级索引的内节点的目录项记录的内容实际上是由三个部分构成的：

• 索引列的值
• 主键值
• 页号

也就是我们把主键值也添加到二级索引内节点中的目录项记录了，这样就能保证B+树每一层节点中各条目录项记录除页号这个字段外是唯一的，所以我们为c2列建立二级索引后的示意图实际上应该是这样子的：

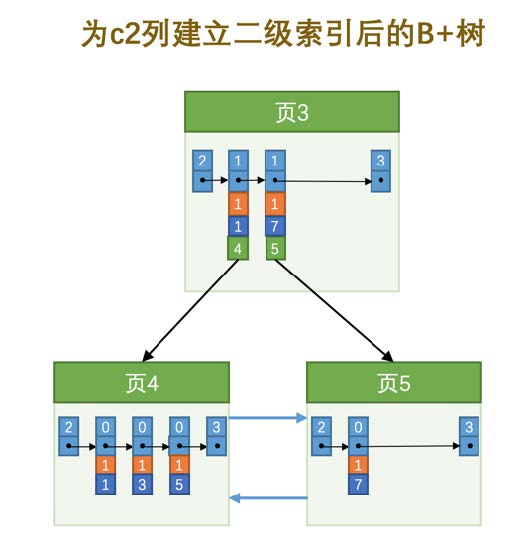
这样我们再插入记录(9, 1, 'c')时，由于页3中存储的目录项记录是由c2列 + 主键 + 页号的值构成的，可以先把新记录的c2列的值和页3中各目录项记录的c2列的值作比较，如果c2列的值相同的话，可以接着比较主键值，因为B+树同一层中不同目录项记录的c2列 + 主键的值肯定是不一样的，所以最后肯定能定位唯一的一条目录项记录，在本例中最后确定新记录应该被插入到页5中。

2.3. 一个页面最少存储2条记录

我们前边说过一个B+树只需要很少的层级就可以轻松存储数亿条记录，查询速度杠杠的！这是因为B+树本质上就是一个大的多层级目录，每经过一个目录时都会过滤掉许多无效的子目录，直到最后访问到存储真实数据的目录。那如果一个大的目录中只存放一个子目录是个啥效果呢？那就是目录层级非常非常非常多，而且最后的那个存放真实数据的目录中只能存放一条记录。费了半天劲只能存放一条真实的用户记录？逗我呢？所以InnoDB的一个数据页至少可以存放两条记录。

3. MyISAM中的索引方案简单介绍

MyISAM的索引方案虽然也使用树形结构，但是却将索引和数据分开存储：

• 将表中的记录按照记录的插入顺序单独存储在一个文件中，称之为数据文件。这个文件并不划分为若干个数据页，有多少记录就往这个文件中塞多少记录就成了。我们可以通过行号而快速访问到一条记录。

  MyISAM记录也需要记录头信息来存储一些额外数据，我们以上边唠叨过的index_demo表为例，看一下这个表中的记录使用MyISAM作为存储引擎在存储空间中的表示：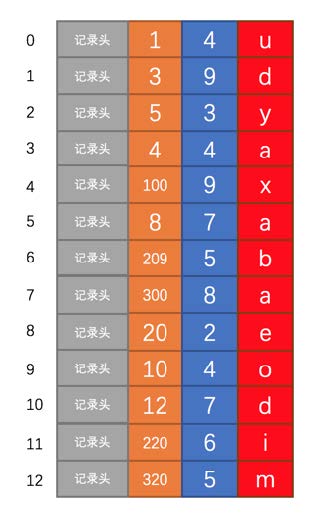

  

  由于在插入数据的时候并没有刻意按照主键大小排序，所以我们并不能在这些数据上使用二分法进行查找。

• 使用MyISAM存储引擎的表会把索引信息另外存储到一个称为索引文件的另一个文件中。MyISAM会单独为表的主键创建一个索引，只不过在索引的叶子节点中存储的不是完整的用户记录，而是主键值 + 行号的组合。也就是先通过索引找到对应的行号，再通过行号去找对应的记录！

  这一点和InnoDB是完全不相同的，在InnoDB存储引擎中，我们只需要根据主键值对聚簇索引进行一次查找就能找到对应的记录，而在MyISAM中却需要进行一次回表操作，意味着MyISAM中建立的索引相当于全部都是二级索引！

  如果有需要的话，我们也可以对其它的列分别建立索引或者建立联合索引，原理和InnoDB中的索引差不多，不过在叶子节点处存储的是相应的列 + 行号。这些索引也全部都是二级索引。

4. MySQL中创建和删除索引的语句

InnoDB和MyISAM会自动为主键或者声明为UNIQUE的列去自动建立B+树索引，但是如果我们想为其他的列建立索引就需要我们显式的去指明。为啥不自动为每个列都建立个索引呢？别忘了，每建立一个索引都会建立一棵B+树，每插入一条记录都要维护各个记录、数据页的排序关系，这是很费性能和存储空间的。

我们可以在创建表的时候指定需要建立索引的单个列或者建立联合索引的多个列：

CREATE TALBE 表名 (
    各种列的信息 ··· , 
    [KEY|INDEX] 索引名 (需要被索引的单个列或多个列)
)

其中的KEY和INDEX是同义词，任意选用一个就可以。我们也可以在修改表结构的时候添加索引：

ALTER TABLE 表名 ADD [INDEX|KEY] 索引名 (需要被索引的单个列或多个列);

也可以在修改表结构的时候删除索引：

ALTER TABLE 表名 DROP [INDEX|KEY] 索引名;

比方说我们想在创建index_demo表的时候就为c2和c3列添加一个联合索引，可以这么写建表语句：

CREATE TABLE index_demo(
    c1 INT,
    c2 INT,
    c3 CHAR(1),
    PRIMARY KEY(c1),
    INDEX idx_c2_c3 (c2, c3)
);

在这个建表语句中我们创建的索引名是idx_c2_c3，这个名称可以随便起，不过我们还是建议以idx_为前缀，后边跟着需要建立索引的列名，多个列名之间用下划线_分隔开。

如果我们想删除这个索引，可以这么写：

ALTER TABLE index_demo DROP INDEX idx_c2_c3;、